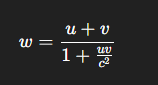A Física Clássica, desenvolvida entre os séculos XVII e XIX, descreve o mundo com base em leis determinísticas e intuitivas, aplicáveis a escalas cotidianas de velocidade, tamanho e energia. Seus pilares são a Mecânica Newtoniana, o Eletromagnetismo de Maxwell e a Termodinâmica Clássica. Esses conceitos explicam desde o movimento de planetas até o funcionamento de máquinas térmicas, assumindo que o espaço e o tempo são absolutos, iguais para todos os observadores.
No início do século XX, experimentos e fenômenos que não podiam ser explicados pela Física Clássica abriram caminho para a Física Moderna. Surgiram então a Teoria da Relatividade (Einstein) e a Mecânica Quântica (Planck, Bohr, Schrödinger, Heisenberg, entre outros). Essas teorias reformularam a compreensão do espaço, do tempo, da energia e da matéria, mostrando que as leis clássicas são apenas uma aproximação válida em condições comuns, mas insuficiente em velocidades próximas à da luz, em campos gravitacionais intensos ou em escalas atômicas e subatômicas. Enquanto a Física Clássica trata partículas como pontos materiais com trajetórias bem definidas, a Física Moderna revela um universo probabilístico, onde partículas podem ter propriedades de ondas e o tempo pode dilatar ou se contrair dependendo do referencial. Essa revolução conceitual não só expandiu o entendimento do cosmos, como também possibilitou tecnologias como GPS, lasers, semicondutores e energia nuclear.
Velocidade relativa na Física Moderna
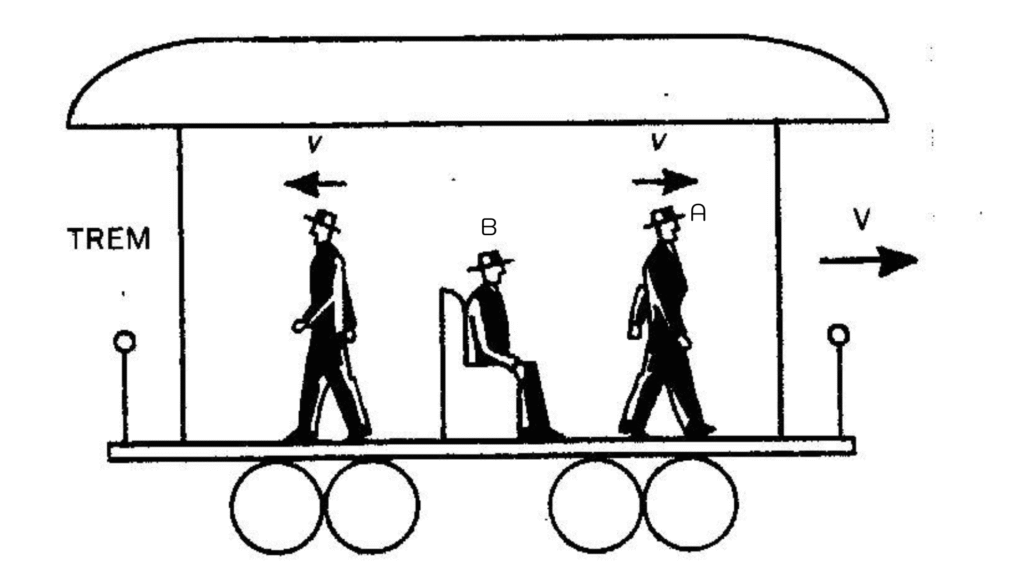
Imagine um trem que se desloca a 80 km/h em relação ao solo. Dentro do trem, um passageiro A caminha no corredor em direção à frente do vagão a uma velocidade de 5 km/h em relação ao próprio trem. Já o passageiro B permanece sentado, portanto sua velocidade em relação ao trem é 0 km/h. Assim, a velocidade relativa de A em relação a B, tomando o referencial do próprio trem, é de 5 km/h. Em outras palavras, para quem está dentro do vagão, o passageiro A se move a 5 km/h em relação ao passageiro B.
Esse raciocínio mostra que, para baixas velocidades, basta somar ou subtrair vetorialmente as velocidades observadas em um mesmo sistema de referência. O trem, nesse caso, é considerado um referencial inercial, desde que se mova com velocidade constante e sem acelerações bruscas. Quando olhamos para esse fenômeno pela perspectiva da Física Moderna, surgem diferenças importantes, mas apenas em situações extremas. A Teoria da Relatividade Restrita, formulada por Albert Einstein em 1905, mostra que, em velocidades próximas à da luz, a simples soma ou subtração não se aplica mais, pois o tempo e o espaço se ajustam para garantir que nada com massa ultrapasse a velocidade da luz. Nesses casos, utiliza-se a fórmula relativística de adição de velocidades, que corrige o cálculo para que os resultados sejam coerentes com os limites impostos pela natureza.
No entanto, para velocidades do cotidiano — como a de um trem ou de uma pessoa caminhando — os efeitos relativísticos são tão pequenos que podem ser desconsiderados, tornando a Física Clássica totalmente suficiente para descrever a situação. Assim, o estudo da velocidade relativa entre passageiros em um trem é um exemplo prático que ilustra a validade da Física Clássica no dia a dia, mas também mostra como conceitos mais profundos da Física Moderna podem se tornar relevantes em condições extremas de alta velocidade.
Se dois objetos A e B se movem em linha reta, com B se movendo a uma velocidade v em relação a A, e A se movendo a uma velocidade u em relação a um referencial inercial, a velocidade w de B em relação a esse referencial é dada por:
Essa é a fórmula relativística de adição de velocidades. Quando u e v são muito menores que c, o termo no denominador é desprezível, e recuperamos a soma clássica onde w=u+v.
Implicações
Limite superior: Nenhum objeto com massa pode atingir ou ultrapassar a velocidade da luz, independentemente de quantos referenciais se somem.
Dilatação temporal e contração espacial: Para que essa restrição se mantenha, o tempo e o espaço se ajustam. Um observador vê relógios em movimento mais lentos (dilatação do tempo) e objetos em movimento mais curtos na direção do movimento (contração de Lorentz).
Transformações de Lorentz: Substituem as transformações de Galileu para lidar com altas velocidades, garantindo que as leis da Física sejam as mesmas para todos os referenciais inerciais.
Neste post pincelamos conceitos que são abordados mais profundamente conforme se mergulha na imensidão que é o conhecimento introduzido pela Relatividade restrita e relatividade espacial elaborada por Einstein. Quer saber mais desses conceitos ? Continue acessando nossos posts.
Acesse nossas redes sociais.